| Markup | Result |
|---|
| 1. | [tex style="background: #ccc; padding: 6px;"]\displaystyle
\Red{\displaystyle e^x=\sum_{n=0}^\infty\frac{x^n}{n!},\ }\Green{\displaystyle e^x=\sum_{n=0}^\infty\frac{x^n}{n!},\ }
\Blue{\displaystyle e^x=\sum_{n=0}^\infty\frac{x^n}{n!}}
[/tex] |
The colordvi package is used by default, so you can use named colors:
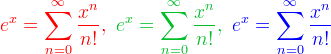 |
| 2. | [preamb]
\newcommand{\mycolor}[1]{\Color{0.7 0.8 0.3 0}{#1}}
[/preamb]
[tex]\displaystyle\mycolor{e=\lim_{x\to +\infty}\left(1+\frac{1}{x}\right)^x}[/tex] |
Of course, you can define your own colors!
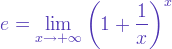 |
| 3. | [preamb]\DeclareMathOperator{\tr}{tr}[/preamb] | This just adds to the  preamble of this page. Nothing should show. preamble of this page. Nothing should show. |
| 4. | The trace of a square matrix [tex]A[/tex], denoted [tex]\tr A[/tex], is the sum of the elements on its main diagonal. | The trace of a square matrix  , denoted , denoted 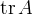 , is the sum of the elements on its main diagonal. , is the sum of the elements on its main diagonal.
Note: this uses the macro
\tr defined in the preamble. |
| 5. | [tex]\mathbb{R}^n[/tex] | 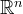 |
| 6. | [tex fontsize="16"]\mathbb{R}^n[/tex] | 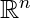 |
| 7. | [tex fontsize="8"]\mathbb{R}^n[/tex] | 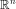 |
| 8. | [tex]x_1+x_2+\cdots+x_n[/tex] | 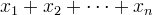 |
| 9. | [tex]F_{n+1}=\sum_{k=0}^n{n-k \choose k}[/tex] | 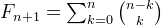 |
| 10. | [tex]\displaystyle F_{n+1}=\sum_{k=0}^n{n-k \choose k}[/tex] | 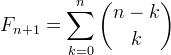 |
| 11. | [tex]n!=n(n-1)(n-2)\cdots 1[/tex] | 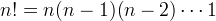 |
| 12. | [tex]\displaystyle (a+b)^n=\sum_{k=0}^n{n\choose k}a^kb^{n-k}[/tex] | 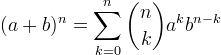 |
| 13. | [tex]\begin{array}{rcl}
(x+y)(x-y)&=&x^2-xy+yx-y^2\\
&=&x^2-y^2;\\
(x+y)^2&=&x^2+2xy+y^2&
\end{array}[/tex] | 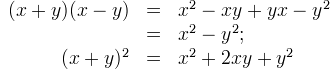 |
| 14. | [tex style="padding: 4px; border-top: 2px solid #3333ff; border-bottom: 2px solid #3333ff; background: #aaaaee;"]\Red{\det(h_{\lambda_i-i+j})=\pm \det(e_{\mu_i-i+j})}[/tex] | 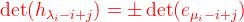 |
| 15. | [tex]\begin{array}{rcl}
\displaystyle\left(\int_{-\infty}^{+\infty}e^{-x^2}dx\right)^2&=&\displaystyle\int_{-\infty}^{+\infty}\!\!\int_{-\infty}^{+\infty}e^{-x^2-y^2}dx\,dy\\
&=& \displaystyle\int_{0}^{2\pi}\!\!\int_{0}^{+\infty}e^{-r^2}r\,dr\,d\theta\\
&=& \displaystyle\int_{0}^{2\pi}\left(\left.-\frac{e^{-r^2}}{2}\right|_{r=0}^{r=\infty}\right)d\theta \\
&=& \pi
\end{array}[/tex] | 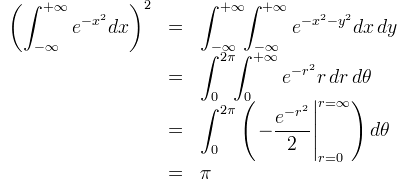 |
| 16. | [tex]\displaystyle \sum_{n=1}^{+\infty}\frac{1}{n^2}=1+\frac{1}{2^2}+\frac{1}{3^2}+\frac{1}{4^2}+\frac{1}{5^2}+\cdots=\frac{\pi^2}{6}[/tex] | 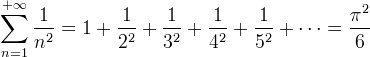 |
| 17. | Meaningful error messages help out with the authoring. | Unparseable or potentially dangerous latex formula. Error 6: Image was not produced or one of its dimensions is too small. \begin{align*}{cc}
(x-y)^2 &=&x^2-2xy-y^2;\\
(x+y)^2 &=& x^2+2xy+y^2
\end{align*} |